Nature of Mott Transition Revealed

Toward Elucidation of the Mechanism of High Temperature Superconductivity

2012.02.15
(2012.03.14 Update)

National Institute for Materials Science

Dr. Masanori Kohno, a MANA Scientist at the International Center for Materials Nanoarchitectonics, National Institute for Materials Science, theoretically clarified the nature of the metal-insulator transition due to electronic correlation (Mott transition).

Abstract

  1. Dr. Masanori Kohno, a MANA Scientist at the International Center for Materials Nanoarchitectonics (MANA; Director-General: Masakazu Aono), National Institute for Materials Science (NIMS; President: Sukekatsu Ushioda), theoretically clarified the nature of the metal-insulator transition due to electronic correlation (repulsive force between electrons) (Mott transition). Dr. Kohno also succeeded in explaining various anomalous behaviors observed in high temperature superconductors in a unified manner as features near the Mott transition. This research is a great advance toward elucidation of the mechanism of high temperature superconductivity.
  2. Because superconductors transmit electricity with no resistance, they are considered key materials for solving environmental and energy problems. However, practical application has been limited by the low superconducting transition temperature of the superconductors obtained up to now. In order to obtain superconductors with higher transition temperatures, it is important to elucidate the mechanism of high temperature superconductivity. Since it is known that high temperature superconductivity is realized near the Mott transition, understanding the anomalous behaviors which occur near the Mott transition is considered to hold the key to elucidating the mechanism of high temperature superconductivity.
  3. In insulators which occur due to the Mott transition (Mott insulators), spin and charge become decoupled, meaning that electron spin can move, but charge cannot move. This spin-charge separation in Mott insulators could not be treated accurately within the framework of conventional metal theory. In the present research, Dr. Kohno applied an analysis of exact solutions for a 1-dimensional system to numerical data obtained using a super computer, and found that 2-dimensional systems also display signs that the degrees of freedom of spin and charge separate toward the Mott transition, and this triggers anomalous behaviors near the Mott transition. Thus, the behaviors that had been thought to be anomalous under the conventional concept can be understood in a natural and unified manner by this new concept as features near the Mott transition in a simple model of a 2-dimensional system. Although this research did not reach an elucidation of the mechanism of high temperature superconductivity, it opens the way to elucidation by solving the mystery of anomalous behavior, which had been the greatest problem in research on high temperature superconductivity.
  4. This research result was obtained as part of the Ministry of Education, Culture, Sports, Science and Technology (MEXT) Grants-in-Aid for Scientific Research, Basic Research (C) “Research on Electronic States Near Mott Transition” (Research Representative: Masanori Kohno), Grant-in-Aid, Special Area “Novel States of Matter Induced by Frustration” (Area Representative: Prof. Hikaru Kawamura, Osaka University), and the World Premier International Research Center Initiative (WPI) International Center for Materials Nanoarchitectonics (MANA; Director-General: Masakazu Aono). The NIMS super computer was used in numerical calculations. This achievement will be announced on February 15 in the online edition of Physical Review Letters, which is a publication of the American Physical Society.
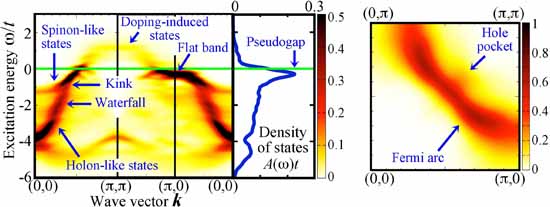
"Figure: Spectral intensity distribution A(k,ω)t of single-electron excitation near the Mott transition in a 2-dimensional Hubbard model. A large intensity area indicates a strong character as a normal electron. In the ordinate at the left, excitation energy ω is divided by the hopping strength t (>0). ω represents the excitation energy in electron-addition excitation for ω>0 and that in electron-subtraction excitation shown with a minus sign for ω<0. The abscissa shows the wave vector k. In the figure at the left, the right-hand panel shows the density of states of single electron excitation A(ω)t. The figure at the right shows the distribution of spectral intensity for ω≈0." Image

Figure: Spectral intensity distribution A(k,ω)t of single-electron excitation near the Mott transition in a 2-dimensional Hubbard model. A large intensity area indicates a strong character as a normal electron. In the ordinate at the left, excitation energy ω is divided by the hopping strength t (>0). ω represents the excitation energy in electron-addition excitation for ω>0 and that in electron-subtraction excitation shown with a minus sign for ω<0. The abscissa shows the wave vector k. In the figure at the left, the right-hand panel shows the density of states of single electron excitation A(ω)t. The figure at the right shows the distribution of spectral intensity for ω≈0.